What is Sound Pressure Level (SPL)?

What is Sound Pressure Level (SPL)? If a tree falls in a forest…? You know the age old philosophical gem. When it comes down to it, sound is about motion. The tree falls, vibrating the air molecules around it. Those air molecules disturb other air molecules and this push/pull continues until the air near our ear registers the sound. So, what if there’s no one there to hear it?

Thanks to science and audio engineering, we have a definitive answer to this existential question. The truth is, we don’t need an ear – just a way to make a measurement and an inference about the original disturbance. One way is to look at the pressure the air exerts on the ear. Fun fact (for nerds like me): our ears are always under considerable, constant pressure. A standard unit used to measure this pressure is the Pascal (Pa) and standard barometric pressure, at sea level, is 101.3kPa (a little over 100,000 Pa).

But what makes sound register is variations in this pressure. The human ear is an incredible instrument. The threshold for human hearing is typically considered to be a variation of 20mPa (a mPa is a millionth of a Pascal) while the threshold of pain for hearing can vary but is around 20Pa. So, we can sense sounds between under 1 billionth to less than 1 thousandth of the standard pressure of the air continually around us. These don’t even register on a standard linear graph, like this one. Another interesting aspect of hearing is that we perceive these changes in ratios. That is, we sense the change in pressure level from 20mPa to 40mPa, similarly to a change from 10Pa to 20Pa (which is half a million times larger!). Think about this the next time you say, “Fractions are hard.” It’s the way you experience life!

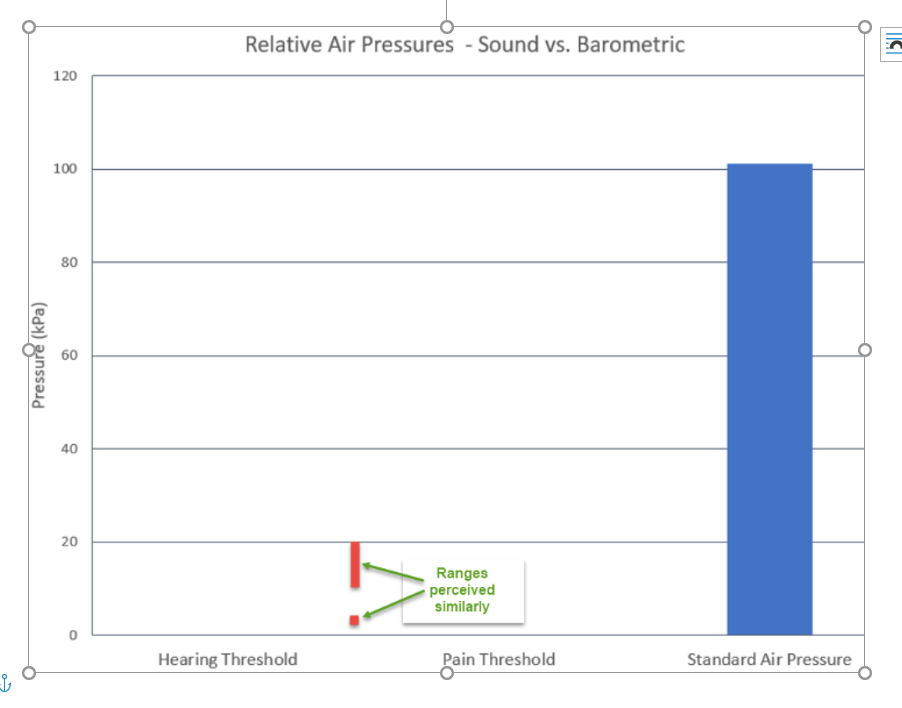
So, how do you measure a phenomenon with this range and fractional nature? Enter the audio engineers with their freaky math and science…

SPL is typically measured using decibels (dB), which are derived by considering the ratio of a given pressure with some reference pressure. A convenient choice for our reference is the standard threshold of hearing, 20mPa. Now, this fraction addresses the relative nature of human hearing. And a high school mathematical tool – the logarithm – allows us to compress the exceedingly wide range to a more manageable scale. To calculate SPL in dB (more precisely dB_SPL to denote the reference being the human threshold of sound detection – other correction factors are also used, like dBA or dBC, to be discussed in another blog), we use the formula:

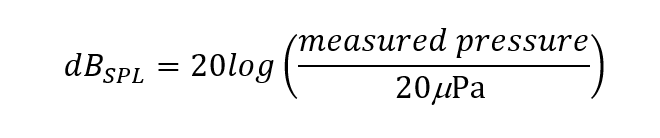
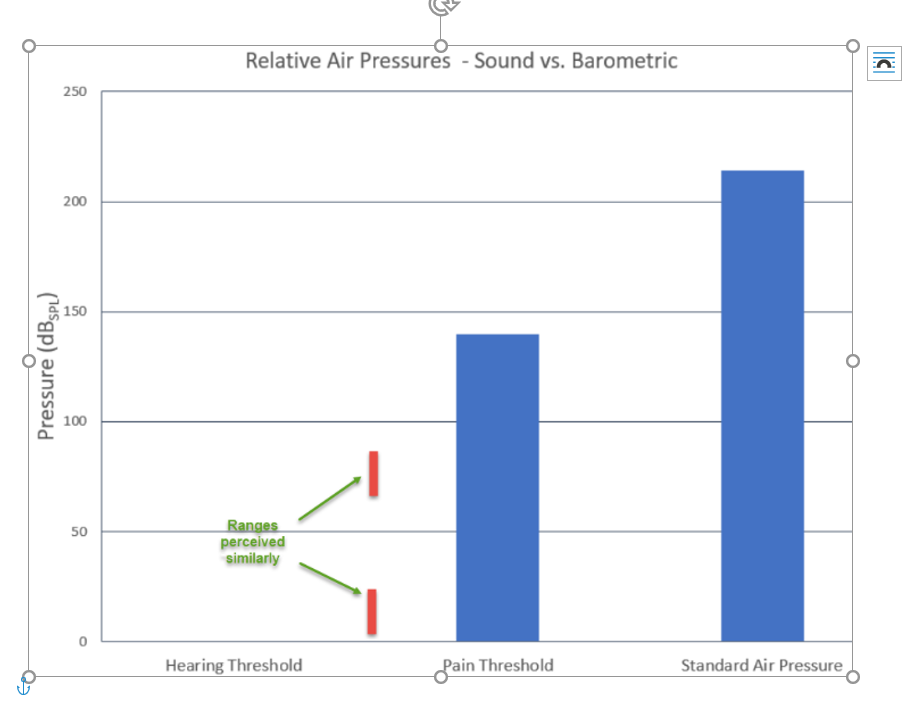
 Using this calculation, with the threshold of human detection and standard barometric pressure as the lower and upper limits, respectively, provides a scale ranging from 0dB_SPL to a bit over 200dB_SPL. The threshold of human hearing is the lower limit and the threshold of pain lies about 2 thirds of the way up. This is a more manageable scale than the nine orders of magnitude in pressure it covers and a difference between 5dB_SPL and 25dB_SPL is experienced in a similar way to a change between 60dB_SPL and 80dB_SPL.

Typical measuring instruments provide measurements in dB_SPL but it’s a simple mathematical calculation to determine what the pressure variation is. So, one of these meters is all we need to determine if the tree actually fell. No need for our ears. Just an instrument that measures pressure in a similar fashion. I suppose one could ask, “But who reads the instrument, to know there’s a sound.